AVL TREE & B – TREE
AVL
– TREE
AVL TREE merupakan kepanjangan dari Adelson Veleskii Landis
Tree. AVL Tree adalah Binary Search Tree yang memiliki perbedaan tinggi/ level
maksimal 1 antara subtree kiri dan subtree kanan. Dengan
Balanced Binary Search Tree, kita dapat membuat suatu tree dengan tinggi
minimum. Untuk menetapkan tingginya, kita dapat menggunakan rumus berikut:
O(log n)
Penerapan struktur data AVL tree digunakan pada Binary Search
Tree bertujuan untuk menyeimbangkan tree tersebut, sehingga waktu pencarian dan
struktur tree dapat disederhanakan.
Insert AVL TREE
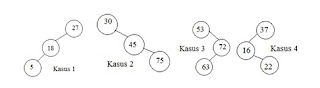
Ada 4 kasus yang biasanya terjadi saat operasi insert
dilakukan, yaitu :
1. Kasus 1 :
node terdalam terletak pada subtree kiri dari anak kiri T (left-left)
2. Kasus 2 :
node terdalam terletak pada subtree kanan dari anak kanan T (right-right)
3. Kasus 3 :
node terdalam terletak pada subtree kanan dari anak kiri T (right-left)
4. Kasus 4 :
node terdalam terletak pada subtree kiri dari anak kanan T (left-right)
T adalah node yang harus diseimbangkan kembali.
4 kasus tersebut dapat diselesaikan dengan melakukan rotasi
yaitu:
1. Kasus 1 dan
2 dengan single rotation
2. Kasus 3 dan
4 dengan double rotation
Single rotation
Single rotasi (rotasi 1x) dilakukan apabila searah, left-left
atau right-right.
Contoh Single Rotation :
Jika suatu Tree diinsert node baru dengan nilai 12, maka akan
terjadi ketidak seimbangan dan hal ini terletak pada posisi root.
Double rotation
Double rotasi (rotasi 2x) dilakukan apabila searah,
left-right atau right-left.
Contoh Double Rotation :
Gambar
diatas merupakan kasus left – right
Delete AVL TREE
Deletion dalam AVL Tree sama seperti teknik deletion dalam
binary search tree yang tidak seimbang.
Ada 2 kasus yang biasanya terjadi saat operasi delete
dilakukan yaitu :
1. Jika node
yang akan dihapus berada pada posisi leaf atau node tanpa anak, maka dapat
langsung di hapus.
2. Jika node
yang akan dihapus memiliki anak, maka proses penghapusannya harus di cek
kembali untuk menyeimbangkan Binary Search Tree dengan perbedaan tinggi / level
maksimal 1.
Anggap T adalah node yang harus diseimbangkan kembali
·
Kasus 1 : node terdalam terletak pada subtree kiri
dari anak kiri T (left-left)
·
Kasus 2 : node terdalam terletak pada subtree kanan
dari anak kanan T (right-right)
·
Kasus 3 : node terdalam terletak pada subtree kanan
dari anak kiri T (right-left)
·
Kasus 4 : node terdalam terletak pada subtree kiri
dari anak kanan T (left-right)
Contoh:
B - TREE
Delete
Sumber:
https://socs.binus.ac.id/2016/12/20/insertion-avl-tree/
https://socs.binus.ac.id/2017/05/15/deletion-avl-tree/
http://strukturdatatugas.blogspot.com/2016/05/rangkuman-pertemuan-6.html
http://sysbreaker.blogspot.com/2014/05/b-tree-dan-heap-deap-tree.html
http://alecatmadja.blogspot.com/2011/06/2-3-tree-part-1.html
http://nurahman11.blogspot.com/2011/06/deletion-2-3-tree.html
https://www.geeksforgeeks.org/2-3-trees-search-and-insert/
B-Tree merupakan pengembangan dari
2-3 Tree. Sehingga aturan-aturan yang berlaku pun mirip.
Berikut beberapa hal yang perlu
diketahui mengenai B-Tree:
·
M adalah jumlah order tree tersebut. (Contoh: order 4
mempunyai maksimal 3 node dan 4 child).
·
Semua "Leaf" berada level yang sama.
·
Setiap Node (kecuali root) punya minimal M/2 children.
·
Root memiliki paling tidak 2 children (bila bukan
leaf)
·
Node tanpa leaf dengan k anak mengandung kunci k-1
·
Semua data yang disimpan dalam urutan yang diurutkan.
2 – 3 Tree
2-3 Tree adalah salah satu tipe
struktur data, dimana setiap node dengan anaknya, memiliki 2 children dan 1
elemen data (2 node) atau 3 children dan 2 elemen data (3 node).
Sifat-sifat 2-3 Tree :
·
Setiap non-leaf terdapat 2-node atau 3-node. Sebuah
2-node berisi satu item data dan memiliki dua anak/children (anak kiri dan anak
tengah). Sebuah 3-node berisi dua item data dan memiliki 3 anak/children (anak
kiri, tengah, dan kanan).
·
Semua leaf berada di level yang sama (level
bawah/bottom level).
·
Semua data yang disimpan akan diurutkan :
o Misalkan A
adalah data yang tersimpan di 2-node. Subtree kiri harus berisi data yang
nilainya lebih kecil dari A. Subtree tengah harus berisi data yang nilainya
lebih besar dari A.
o Misalkan A
dan B adalah data yang tersimpan di 3-node. Subtree kiri harus berisi data yang
nilainya kurang dari A. Subtree tengah berisi nilai antara A dan B, dan subtree
kanan berisi nilai yang lebih dari B.
Contoh :
Gambar diatas merupakan contoh 2 –
node yaitu node yang berisi 1 data dan mempunyai 2 child
Insert
Syarat insertion yaitu:
·
Pertama tentukan dahulu dimana key akan diletakkan
menggunakan algoritma search, key pasti ditempatkan pada node leaf.
·
Jika node tadi adalah 2-node, maka letakkan saja key
tersebut disitu.
·
Jika nodenya adalah 3-node, maka jadikan data tengah
dari key, A, dan B (A dan B adalah data yang sudah ada sebelumnya di dalam
node), menjadi parent, dan split 2 data tersisa menjadi 2 buah 2-node. Cek
apakah parent adalah 3-node, jika iya maka ulangi langkah 3 sampai parent
menjadi 2-node.
Contoh:
Delete
Syarat Deletion yaitu:
·
Tentukan di node mana data yang ingin dihapus
·
Jika berada dalam 3-node, langsung hapus saja datanya.
·
Jika berada dalam 2-node :
o Jika parent
adalah 3-node : ambil satu data dari parent.
Jika sibling adalah 3-node, ambil salah satu data nya untuk dijadikan data pada parent (agar parent
menjadi 3-node lagi).
Jika sibling adalah 2-node, buat parent menjadi 2-node dengan
menggabungkan (merge) sibling dengan node tempat data didelete.
o Jika parent
adalah 2-node : Jika sibling adalah 3-node, turunkan data parent ke node dan
ambil satu data dari sibling untuk menggantikan parent. Jika sibling 2-node,
gabungkan sibling dengan node yang dihapus datanya.
Contoh:
Pada gambar diatas, misalkan yang
ingin di delete adalah angka 15 maka langsung di hapus karena 15 merupakan
leaf.
Sumber:
https://socs.binus.ac.id/2016/12/20/insertion-avl-tree/
https://socs.binus.ac.id/2017/05/15/deletion-avl-tree/
http://strukturdatatugas.blogspot.com/2016/05/rangkuman-pertemuan-6.html
http://sysbreaker.blogspot.com/2014/05/b-tree-dan-heap-deap-tree.html
http://alecatmadja.blogspot.com/2011/06/2-3-tree-part-1.html
http://nurahman11.blogspot.com/2011/06/deletion-2-3-tree.html
https://www.geeksforgeeks.org/2-3-trees-search-and-insert/